Electroaimant :
Tout fil conduisant du courant électrique crée autour de lui un champ magnétique qui s’enroule autour du fil selon la règle de la main droite :
Schéma représentant la règle de la main droite.

(source image : http://bv.alloprof.qc.ca/s1177.aspx)
Lorsque l’on enroule la main droite autour du fil avec le pouce orienté dans le sens du courant, le sens de rotation des doigts autour du fil nous montre l’orientation du champ magnétique produit par le courant électrique traversant le fil.
En enroulant les fils sous la forme de spires, la bobine formée se comporte comme un dipôle magnétique lorsqu’elle est sous tension, le champ magnétique étant plus intense aux niveaux des spires.
Schéma représentant le champ magnétique créé par une spire de courant.

(source image : http://patrick.kohl.pagesperso-orange.fr/spectro_part/spectro_part_2_1.htm)
Schéma représentant le champ magnétique créé par une bobine de courant.
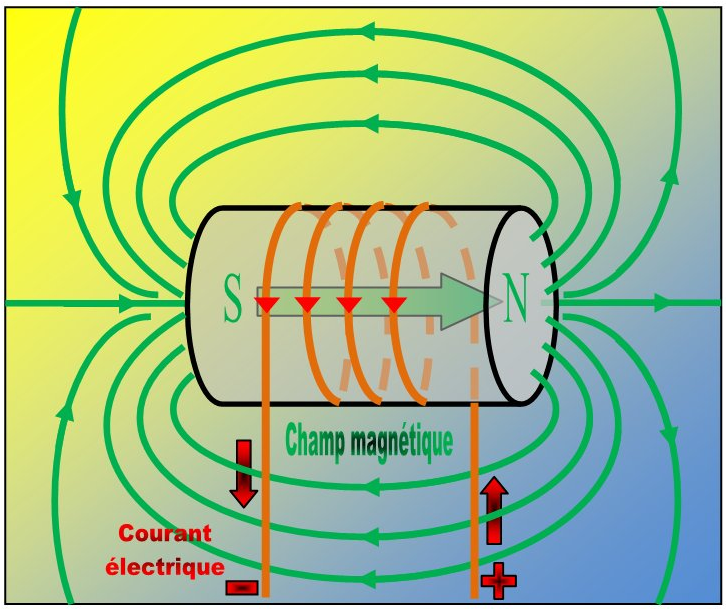
(source image : http://e.m.c.2.free.fr/magnetostatique1.htm)
On peut également appliquer la règle de la main droite : on enroule la main avec les doigts dans le sens du courant qui traverse la spire et l’orientation du pouce nous donne la direction du champ magnétique sur l’axe de la spire. La polarité d’une bobine change donc selon le sens du courant.
L’intensité du champ magnétique sur l’axe de la bobine dépend de sa forme. Si la bobine est dite “plate”, c’est à dire avec un rayon plus grand que sa longueur, elle peut alors être assimilée à une seule spire de courant, on a alors:
![]() avec B l’intensité du champ magnétique en Tesla; la perméabilité magnétique du milieu (S.I); N le nombre de spires; I l’intensité du courant électrique traversant les spires en Ampère et α l’angle entre la bobine et son axe au point M.
avec B l’intensité du champ magnétique en Tesla; la perméabilité magnétique du milieu (S.I); N le nombre de spires; I l’intensité du courant électrique traversant les spires en Ampère et α l’angle entre la bobine et son axe au point M.
Schéma représentant différentes valeurs entrant en jeu dans le calcul du champ magnétique produit par une spire de courant :

(source image : http://e.m.c.2.free.fr/magnetostatique1.htm )
En revanche s’il s’agit d’un solénoide, c’est à dire d’une bobine plus longue que large alors on a :
![]() avec a min le nombre de spires par unité de longueur; αmin l’angle entre l’axe et la face la plus éloignée du point M, en M et αmax l’angle entre l’axe et la face la plus proche du point M, en M.
avec a min le nombre de spires par unité de longueur; αmin l’angle entre l’axe et la face la plus éloignée du point M, en M et αmax l’angle entre l’axe et la face la plus proche du point M, en M.
Schéma en coupe d’un solénoïde représentant les différentes valeurs en jeu dans le calcul du champ magnétique produit par un solénoïde :

(source image : http://e.m.c.2.free.fr/magnetostatique1.htm )
(sur le schéma αmin =Θ2 et αmax = Θ1)
Dans un premier temps on constate que l’intensité du champ magnétique d’une bobine est proportionnelle à l’intensité du champ magnétique du milieu, dans le vide ou dans l’air cette valeur est de :
![]() . C’est donc une valeur extrêmement faible, cependant cette valeur va être nettement plus élevée dans d’autres matériaux. Ainsi, si l’on introduit un noyau en matériaux ferromagnétique comme du fer au centre de la bobine, celui ci va concentrer les lignes de champ, ce qui se traduit par une valeur de la perméabilité magnétique et donc de l’intensité du champ magnétique beaucoup plus élevée. Nous avons par exemple pu constater lors de nos expériences qu’au dessus d’une bobine sans noyau le ferrofluide ne réagissait pas, en revanche, sur la même bobine avec la même intensité du courant électrique, mais en plaçant un noyau ferreux au centre de la bobine, le ferrofluide forme des pics.
. C’est donc une valeur extrêmement faible, cependant cette valeur va être nettement plus élevée dans d’autres matériaux. Ainsi, si l’on introduit un noyau en matériaux ferromagnétique comme du fer au centre de la bobine, celui ci va concentrer les lignes de champ, ce qui se traduit par une valeur de la perméabilité magnétique et donc de l’intensité du champ magnétique beaucoup plus élevée. Nous avons par exemple pu constater lors de nos expériences qu’au dessus d’une bobine sans noyau le ferrofluide ne réagissait pas, en revanche, sur la même bobine avec la même intensité du courant électrique, mais en plaçant un noyau ferreux au centre de la bobine, le ferrofluide forme des pics.
On constate aussi que l’intensité du champ magnétique est proportionnelle à l’intensité du courant traversant les spires, il est donc facile de la faire varier. Lors de nos montages nous avons utilisé un générateur de tension continu, relié en série à la bobine, à une boite à décade puis un ampèremètre. Nous avons donc progressivement baissé la résistance du circuit pour nous aligner sur l’intensité maximale de la bobine, soit 0,6A. Comme dans l’expérience déjà citée, on constate que plus l’intensité du courant est forte plus les pics formés sont nombreux, hauts et denses. Dans le cadre d’une pompe cardiaque, un simple circuit électrique avec un interrupteur calé sur une fréquence cardiaque constante, suffirait donc à faire fonctionner la pompe.
Cependant la valeur de l’intensité magnétique d’une bobine sur son axe diminue très rapidement avec la distance. Connaissant les dimensions de notre bobine, il est possible d’évaluer l’évolution de l’intensité du champ magnétique sur son axe avec la distance. Notre appareil compte 1300 spires, d’un diamètre de 6 cm, sur une longueur de 5,5 cm et avec un intensité maximum de 0,6 A. Elle est à mi-chemin entre une bobine plate et un solénoide, nous allons donc faire le calcul des deux façons.
Graphique 1:
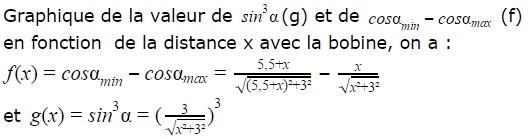
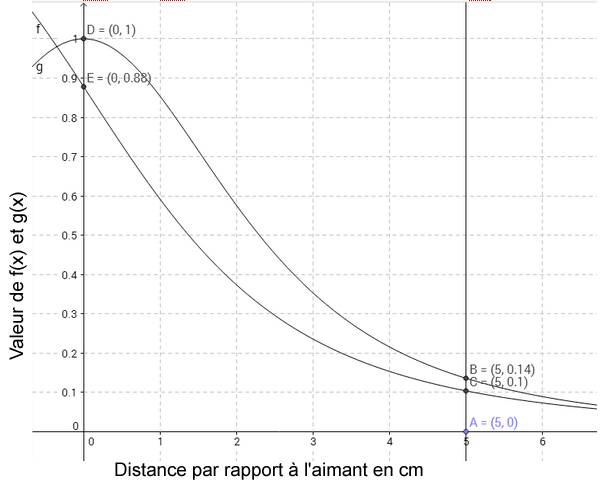
(graphique réalisé à l’aide de l’outils mathématique géo-gebra)
On constate tout d’abord que l’allure des deux courbe est similaire, ainsi nous pouvons en conclure que la méthode de calcul importe peu. Ensuite nous remarquons que g et f sont fortement décroissantes et diminuent très rapidement avec la distance, ainsi à une distance x=5cm, cette valeur est
![]() , environ 10 fois moins importante qu’au niveau de la bobine.
, environ 10 fois moins importante qu’au niveau de la bobine.
L’intensité du champ magnétique va alors suivre cette même allure.
graphique 2 :
On a N=1300 spires; I=0,6A; R=3cm et n=1300/0.06 =2,4*10^4 spires/m. On peut aussi mesurer la valeur de µ avec le noyau ferreux. Nous avons mesuré un champ magnétique de 12mT au bord de la bobine on a donc :
![]()
(on constate au passage que d’après les valeurs mesurées l’ajout d’un noyau n’a pas changé grand chose à la valeur de la perméabilité magnétique du milieu)
Représentation de la valeur de l’intensité du champ magnétique en fonction de la distance x avec la bobine :


(graphique réalisé à l’aide de l’outils mathématique géo-gebra)
Ainsi à 5cm de notre bobine la valeur de l’intensité du champ magnétique est 10 fois moins importante qu’aux bords (de l’ordre du mT).
De façon plus générale, l’intensité du champ magnétique en dehors d’un solénoide est souvent considérée comme nul en comparaison à celle mesurée à l’intérieur.
Lien avec notre projet:
On constate que l’intensité du champ magnétique produit par une bobine à l’extérieur de celle ci peut être suffisante pour attirer l’aiguille d’un boussole (dans notre cas elle est de 1 mT à une distance de 5 cm contre seulement 50.10^-6 T pour le champ magnétique terrestre), ou même pour pouvoir observer la formation de pics avec notre ferrofluide.
En revanche, dans une pompe, il faut que le ferrofluide soit attiré de façon conséquente par l’aimant afin d’exercer une force non négligeable sur le liquide à l’intérieur de la pompe dans le but d’observer une variation de la pression. Le fait est que la force magnétique entre deux dipôles étant fonction de l’intensité du champ magnétique, il convient de posséder un équipement conséquent avec une grosse bobine et un noyau ayant une valeur de perméabilité magnétique plus élevé. Il faudrait aussi appliquer un courant électrique beaucoup plus intense, ce qui pourrait avoir des conséquences extrêmement néfastes sur l’organisme en cas de court circuit.
Lors de nos TP nous avons cherché à mesurer l’évolution de cette force magnétique en fonction de la distance. Nous avons donc suspendu notre pilulier rempli de ferrofluide à un dynamomètre puis placé un aimant produisant un champ magnétique d’intensité maximum environ 1T à différentes distances du pilulier. Nous avons ensuite mesuré l’écart d’accélération entre le moment où l’aimant est placé loin du pilulier (trop loin pour exercer une quelconque attraction sur lui) et le moment où il est assez près pour que le pilulier vienne ensuite à son contact. Placé entre 2,5 et 1,5 cm du pilulier, l’aimant exerce une force d’environ 0,25 N sur le pilulier, ce qui n’est pas suffisant pour qu’il vienne à son contact. A partir de 0,5 cm, l’aimant exerce une force de 0,8N sur le pilulier et celui-ci se colle complètement à l’aimant.
On constate que pour pouvoir observer cette force magnétique il faut que l’aimant soit placé très près du pilulier et cette force reste de toute façon faible. De plus dans une pompe cette force magnétique devra s’opposer à la force de résistance élastique des deux membranes et à la viscosité dynamique du sang, plus élevée que celle de l’eau et de l’air (6.10^-3 Pa.s > 1.10^-3 Pa.s > 1,8.10^-5 Pa.s). Dans notre pompe le ferrofluide devra aussi être éloigné de plusieurs centimètres de façon à respecter un volume d’éjection systolique d’au moins 75mL pour chaque ventricule.
- La construction de la pompe s’oppose donc à deux problèmes de taille que sont la faible intensité du champ magnétique produit par une bobine à l’extérieur de celle-ci, et la décroissance rapide de l’intensité du champ magnétique et donc de la force magnétique pour une même aimantation lorsque l’on s’éloigne d’un aimant (sachant que dans notre cas, cette décroissance est encore plus marquée puisque l’aimantation du ferrofluide dépend de l’intensité du champ magnétique).
Toutes ces études ont été réalisées avec l’aide de ferrofluide que nous avons nous même synthétisé.

